Despite its low gravitational acceleration of only 3.72 [m/s²], our neighbor planet is much less favorable for flying because of its atmosphere density, which is around 80 times lower.

Based on basic equations of lift and drag forces, we can do rough estimation of the aerodynamics. The required power for leveled flight is given by the following equation, where &rho is air density, S wing area, v flight speed and C_L and C_D the lift and drag coefficients.

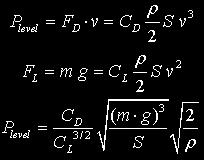
If we assume that the airplane mass m is proportional to wing area S, we get:

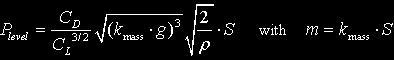
This rough estimation shows us, considering that the solar power is proportional to the surface of the wing, that the feasibility of a solar-powered glider does in a first order estimation not depend on the size of the airplane or the flying speed. It is interesting to notice that for the same aerodynamics and the same surface, a flight on Mars will need (g'³/&rho')^1/2 = 2.1 times more power than on Earth. In order to reduce this power, efforts have to be concentrated on the aerodynamics (C_L, C_D) and the weight (m). One more problem is the very low Re number, which increases the difficulty of flight because the boundary layer is much less capable of handling an adverse pressure gradient without separation and the maximum lift capability is restricted.
In order to demonstrate the feasibility of continuous solar powered flight on Mars, we have to define similar flight conditions for experiments on Earth. Mars airplane validation can then be achieved on our planet with a consistent choice of flight altitudes to prove the feasibility of continuous flight (power similitude, speed similitude) and the aerodynamics at low Re numbers (similar Re or flight speed). It is also planned to use special wind tunnel tests with scaled model.